- graspPlugin
- 公開レポジトリ
- graspPluginのインストール方法
- graspPluginのWindowsへのインストール方法 (Choreonoid 1.5)
- CnoidRosプラグイン
- ConstraintIKプラグイン
- GeometryHandlerプラグイン
- Grasp プラグイン解説
- GraspConsumer プラグイン解説
- Graspプラグイン把持姿勢DB生成機能
- MotionFileのコマンド
- MotionFileプラグイン
- Motionタブの使用方法(choreonoid 1.5)
- Motionファイルの作成
- PCL, PCL.rtcプラグイン
- PCLプラグイン位置・姿勢推定機能
- PRM プラグイン解説
- PRMプラグイン
- PickAndPlacePlannerプラグイン
- RobotInterface プラグイン解説
- RobotInterfaceプラグインへのツールチェンジ機能の追加について
- RtcGraspPathPlanプラグイン
- SoftFingerStabilityプラグイン
- kinectキャリブレーション
- pythonスクリプトpythonインターフェース
- フィッティング機能
- 固定されたデプスセンサでのばら積みピッキング
- 把持姿勢補間・配置位置探索
- 把持計画パラメータ設定方法
- Choreonoid プラグインプログラミング Tips
- Downloads
- 古い情報
ConstraintIKプラグイン
水, 10/09/2013 - 16:45 — ohchi
ConstraintIK.hをインクルードします。
サンプルコードを以下に示します。
collisionShape:以下が楕円体情報です。
-center: 楕円体の中心座標
-rpy: 楕円体の回転行列(rpy)
-length: 楕円体の半径
-security_distance: 許容する最小楕円体間距離(文献[1]の(3)式のd_sに相当)
-effective_distance: 楕円体間の拘束条件が有効となる距離(文献[1]の(3)式のd_iに相当)
-xi:(文献[1]の(3)式のξに相当)
-jointName: 対象ジョイント名
-center: 楕円体の中心座標
-rpy: 楕円体の回転行列(rpy)
-length: 楕円体の半径
座標、回転行列はローカル座標系で指定します。
-name: カメラ名
-type: カメラパスの種類(HEAD:頭部カメラ、HAND:ハンドアイカメラ)
-base: カメラパスのベースリンク名
-cameraLink: カメラが設置されているリンク名
-direction: カメラの向き
-focal_distance: カメラの焦点距離(ハンドアイカメラのみ)
-pos: カメラの位置
direction、posはローカル座標系で指定します。
extplugin/graspPlugin/ConstraintIK/project/generate_ellipsoid_test.cnoidを読み込みます(「ファイル」->「プロジェクトの読み込み」)。
ConstraintIKバーの「SaveObstacleShape」を押します。

下記ダイアログが表示されるので、「Clustering:」は「Number of Clusters」を選択し、「Approximation type:」はboundingboxを選択し、「show」ボタンをクリックします。
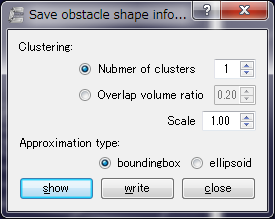
そうすると下図画像のように、対象の箱のエッジに障害物となる楕円体が表示されます。

ダイアログの「write」ボタンをクリックすると「box3.yaml」が生成されます。
生成された「box3.yaml」ファイルをextplugin/graspPlugin/ConstraintIK/project/に移動します。
choreonidを終了します。
1. 基本情報
プラグイン名:ConstraintIK
依存プラグイン:Grasp;GeometryHandler
2. 主な機能・説明
・障害物を避ける、関節角度制約付きのIK。参考文献[1]の3章を実装。
・このプラグインの実装にはEQuadProg++[2]を使用しています。
・障害物は楕円体で近似します。この情報はyamlファイルに記述します。
・ロボットの楕円体と環境の(SetEnvした)オブジェクトの楕円体が衝突しないように制約をかけIKを解きます。
・カメラを設定してあると、アームとカメラを同時にIKを解きます。
2.1. メニュー
- SaveObstacleShape
対象物の楕円体情報を保存する
- DisplayObstacleShape
楕円体を表示
- HideObstacleShape
楕円体表示のクリア
-SetCamera
IKを解く時のカメラを選択する
2.2. 使用方法
2.2.1. IK呼び出し方法
まず、ConstrainIKプラグインを使用できるようにします。ConstraintIK.hをインクルードします。
#include "../ConstraintIK/ConstraintIK.h
サンプルコードを以下に示します。
Vector3 p; // 目標位置
Matrix3 R; // 目標姿勢
// Solverのインスタンスを作成。この時対象となるアームを設定する。
ConstraintIKSolver* cik = new ConstraintIKSolver(PlanBase::instance()->targetArmFinger);
// パラメータの設定(必要な場合)
cik->setStep(10); //現在地から目標付近まで何分割して解くか(デフォルト20)
cik->setMaxIteration(10); //目標付近での微調整の最大回数(デフォルト10)
cik->setFixJoint(0); //固定したい関節を設定します(JointNumを指定 )
cik->setTranslationalJointCoeff(10) //並進関節が回転関節に比べどれくらい動きづらくするか設定します
if(!cik->ik(p,R)){
cerr << "ik failed" << endl;
}
delete cik;
2.2.2. オブジェクトへの障害物(楕円体)の設定
choreonoidから、オブジェクトに障害物となる楕円体を設定する方法を説明します。(ロボットについては下記詳細な説明を参考に手動で設定してください。)
1.対象オブジェクトをSetObjectします。
2.ConstraintIKバーのSaveObstacleShapeをクリックします。
3.ダイアログが表示されるので、分割パラメータ、近似方法選択します。
Clusteringが分割パラメータで、
・Number of Clustersを選択すると指定したクラスタ数に分割された後、楕円体が配置されます。
・Overlap volume ratioを選択するとクラスタ同士の重なりが指定した割合になるように分割された後、楕円体が配置されます。
Approximation typeが楕円体の配置方法で、
・boundingboxを選択するとクラスタのバウンディングボックスの辺に沿うように楕円体が配置されます。
・ellipsoidを選択するとクラスタを2次曲面で近似した時の楕円体が配置されます。(クラスタを2次曲面近似した結果,楕円体とならない場合は表示されません。)
4.showボタンをクリックすると楕円体が表示されます。もし、違う結果が見たい場合はパラメータを変更して再度showボタンをクリックします。
5.設定する楕円体が決定したらwriteボタンをクリックします。
6.[対象物名].yamlが作成されます。yamlファイルの最初の行を確認し、対象のhrpファイルパスと違う場合は修正してください。
2.2.3. ロボットへの障害物(楕円体)の設定
「3.1.2.yamlファイル形式」を参考にし、手動でロボットのyamlファイルに楕円体情報を追加してください。
3.詳細な説明
3.1.yamlファイル形式
3.1.1.オブジェクト
yamlファイルのサンプルを示します。
modelFile: ./boxL1Hrp.wrl
collisionShape:
-
center: [0.2325 , 0 , 0.095]
rpy: [0 , -0 , 0]
length: [0.005 , 0.1475 , 0.005]
security_distance: 0.01
effective_distance: 0.2
xi: 0.1collisionShape:以下が楕円体情報です。
-center: 楕円体の中心座標
-rpy: 楕円体の回転行列(rpy)
-length: 楕円体の半径
-security_distance: 許容する最小楕円体間距離(文献[1]の(3)式のd_sに相当)
-effective_distance: 楕円体間の拘束条件が有効となる距離(文献[1]の(3)式のd_iに相当)
-xi:(文献[1]の(3)式のξに相当)
3.1.2.ロボット
下記のような記述をロボットのyamlファイルに追加します。
collisionShape:
-
jointName: RARM_JOINT2
center: [-0.025, -0.015, -0.1]
rpy: [0, 0, 0]
length: [0.05, 0.05, 0.125]
-
jointName: RARM_JOINT1
center: [-0.025, -0.11, -0.14]
rpy: [0, 0, 0]
length: [0.05, 0.05, 0.12]-jointName: 対象ジョイント名
-center: 楕円体の中心座標
-rpy: 楕円体の回転行列(rpy)
-length: 楕円体の半径
座標、回転行列はローカル座標系で指定します。
3.1.3.カメラ
カメラ情報は下記のような記述をロボットのyamlファイルに追加します。
camera:
-
name: HEADCAMERA
type: HEAD
base: WAIST
cameraLink: HEAD_JOINT1
direction: [1.0, 0.0, 0.0]
pos: [0.09, 0.0, 0.08]
-
name: HANDCAMERA
type: HAND
base: WAIST
cameraLink: LARM_JOINT5
direction: [-1.0, 0.0, 0.0]
focal_distance: 0.5
pos: [-0.02, 0.0, -0.0]
-name: カメラ名
-type: カメラパスの種類(HEAD:頭部カメラ、HAND:ハンドアイカメラ)
-base: カメラパスのベースリンク名
-cameraLink: カメラが設置されているリンク名
-direction: カメラの向き
-focal_distance: カメラの焦点距離(ハンドアイカメラのみ)
-pos: カメラの位置
direction、posはローカル座標系で指定します。
3.2.アルゴリズム
目標位置・姿勢まで20分割して文献[1]のIKを使用して解いていきます。
このままでは、目標位置・姿勢までとの誤差が大きいことがあります。
そのため微調整のため、文献[1]のIKを誤差が十分小さくなるまで繰り返し解きます。
4.動作確認
4.1.障害物(楕円体)の設定
choreonoidを起動します。extplugin/graspPlugin/ConstraintIK/project/generate_ellipsoid_test.cnoidを読み込みます(「ファイル」->「プロジェクトの読み込み」)。
ConstraintIKバーの「SaveObstacleShape」を押します。
下記ダイアログが表示されるので、「Clustering:」は「Number of Clusters」を選択し、「Approximation type:」はboundingboxを選択し、「show」ボタンをクリックします。

そうすると下図画像のように、対象の箱のエッジに障害物となる楕円体が表示されます。

ダイアログの「write」ボタンをクリックすると「box3.yaml」が生成されます。
生成された「box3.yaml」ファイルをextplugin/graspPlugin/ConstraintIK/project/に移動します。
choreonidを終了します。
4.2.障害物(楕円体)の表示
choreonoidを起動します。
extplugin/graspPlugin/ConstraintIK/project/box3.yamlを読み込みます(「ファイル」->「読み込み」->「OpenHRPモデルファイル」)。
アイテムタブのbox3を選択し、Plannerバーの「SetEnv」をクリックします。

ConstraintIKバーの「DisplayObstacleShape」を押し、4.1で設定した楕円体が表示されることを確認します。
ConstraintIKバーの「HideObstacleShape」を押し、楕円体が消えることを確認します。
choreonoidを終了します。
参考文献
[1] 金広 他,"実機の物理的制約を考慮した即応的脚動作生成手法," 日本ロボット学会論文誌, vol. 28, no. 10, pp. 1251-1261, 2010.
[2] EQuadProg++, http://www.cs.cmu.edu/~bstephe1/eiquadprog.hpp.
